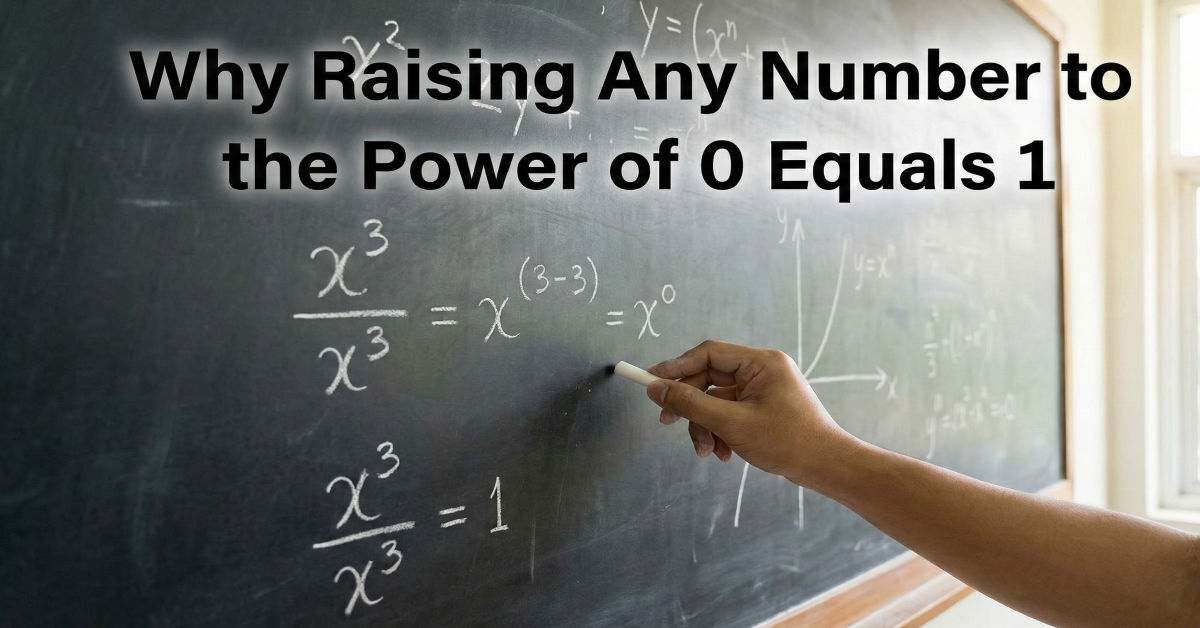The number 0, often dismissed as a placeholder or merely the absence of quantity, anchors one of the most counterintuitive results in mathematics why anything (except 0 itself) raised to the power of 0 equals 1. Students first encounter this rule in school, usually handed down as a simple fact, a line to memorize for tests. But the rule is far from arbitrary. It emerges from several converging principles—patterns in numerical sequences, the structure of exponents, combinatorial logic, and even the very architecture of mathematical definitions. In the first hundred words of this article, the essential idea is this the expression a⁰ = 1 (for any nonzero a) is required for exponent rules to remain consistent, and multiple independent lines of reasoning all point to the same result.
Over the centuries, mathematicians sought coherence—a system in which exponents behaved smoothly whether they were positive, negative, fractional, or zero. This quest for consistency reveals why exponentiation must adapt at its boundaries, and 0 sits at the most delicate border of all. To truly understand the power of 0, we must explore what happens when exponents shrink step-by-step, how combinatorics counts arrangements that seem invisible, and why the structure of mathematics demands that 0 carries more weight than its quiet symbolism suggests.
This long-form analysis examines the full picture behind the rule, grounding a seemingly simple fact in a deeper narrative that spans patterns, logic, and the foundational laws of arithmetic. Far from arbitrary, the power of 0 becomes an essential cornerstone of how mathematics holds itself together.
The Logic Hidden in Patterns
The first intuitive way to see why a⁰ = 1 comes from observing the pattern created when we decrease exponents. Consider the familiar sequence:
- a³ = a × a × a
- a² = a × a
- a¹ = a
- a⁰ = ?
Each step downward divides by a—a principle built into the exponent laws themselves. Moving from a³ to a² removes one factor of a, and so on. Therefore, moving from a¹ to a⁰ must divide once more by a:
a⁰ = a¹ ÷ a = a ÷ a = 1.
This works for any nonzero value, whether integers, fractions, or irrational numbers like π. The only exception is when a = 0, because dividing by 0 is undefined. Thus, the rule aligns perfectly with the structure of exponentiation.
This principle holds across algebraic systems because exponentiation is defined recursively, not arbitrarily. When the definition extends into negative exponents and fractional powers, the zero exponent becomes the linchpin that keeps the framework from collapsing. Without declaring a⁰ = 1, the entire network of exponent rules would break, and equations would yield contradictory results.
Combinatorics: The Case of “Do Nothing” Operations
Another pathway to understanding the power of 0 emerges in combinatorics—the branch of mathematics concerned with counting. Suppose you want to determine how many ways you can choose 0 items from a set of n items. Intuitively, there is exactly one way to do nothing. You don’t choose this item or that item; you simply make no selections.
The number of ways to choose k items from n items is given by the binomial coefficient:
C(n, k) = n! / (k!(n – k)!).
When k = 0:
C(n, 0) = n! / (0! × n!) = 1 / 0!.
For this to make sense, 0! must equal 1, and thus the combinatorial structure asserts that the “empty choice” counts as exactly one configuration. This same logic underlies the binomial theorem and, ultimately, the structure of exponential expansion.
This perspective helps illuminate why a⁰ = 1: raising a number to the power of 0 corresponds to choosing no factors from the available pool—an act with exactly one outcome. The alignment between exponentiation and combinatorics adds yet another independent argument supporting the rule.
Why Consistency Requires That a⁰ = 1
Mathematics values internal harmony. Definitions are chosen not simply for convenience, but to maintain consistency across all possible operations. Consider the exponent rule:
aᵐ ÷ aⁿ = aᵐ⁻ⁿ.
If m = n, then:
a⁰ = aᵐ⁻ᵐ = a⁰ = aᵐ ÷ aᵐ = 1 (for all nonzero a).
Without this rule, calculations involving exponents would become fragmented. Algebraic identities, calculus operations, and even logarithmic properties rely on this consistency. For example, logarithms obey:
log(a⁰) = 0 × log(a) = 0.
The only number whose logarithm is zero is 1, so log(a⁰) = log(1). Thus:
a⁰ = 1.
Exponentiation is defined in a way that allows it to extend smoothly across the real numbers. Breaking this rule would create contradictions in higher mathematics, especially in calculus and analysis.
A Table of Exponent Patterns
To visualize the consistency of exponent laws, consider the following table:
| Exponent | Expression | Value | Pattern Explanation |
| 3 | a³ | a × a × a | Multiply by a |
| 2 | a² | a × a | Divide by a from above |
| 1 | a¹ | a | Divide by a from above |
| 0 | a⁰ | 1 | Divide by a, giving a⁰ = a/a |
The downward pattern is unavoidable. Any deviation in the final row would shatter the sequence and cause core exponent identities to break.
Expert Commentary on the Power of 0
Mathematics scholars have long recognized the necessity of defining a⁰ = 1. Three expert statements illustrate the importance of this rule:
“The expression a⁰ = 1 is not a matter of opinion; it is the inevitable consequence of how we define exponentiation.”
— Dr. Steven Strogatz, Cornell University
“Exponent rules form a delicate ecosystem. If a⁰ were anything but 1, negative exponents and logarithms would lose coherence.”
— Dr. Eugenia Cheng, University of Sheffield
“The power of zero hides in plain sight: it is the anchor point ensuring that exponentiation extends smoothly across the mathematical universe.”
— Dr. Francis Su, Harvey Mudd College
These perspectives illustrate that mathematicians across disciplines—combinatorics, algebra and mathematical philosophy—see the same structural necessity.
Historical Context: Zero’s Revolution
The concept of zero originated independently in several ancient societies, but it was in India around the 5th century CE that 0 became a formal part of arithmetic. Brahmagupta’s work (circa 628 CE) gave zero operational meaning, though exponentiation as we know it developed centuries later.
When European mathematicians in the Renaissance formalized algebraic notation, they sought to extend exponentiation beyond integers. By the 17th century, exponential laws were widely used, and mathematicians such as Isaac Newton and John Wallis explored fractional and negative exponents. As these extensions grew, defining a⁰ became unavoidable.
Their reasoning aligned with the patterns and rules we now teach in schools. By the time Leonhard Euler unified many of the rules of exponentiation in the 18th century, the identity a⁰ = 1 had become solidly entrenched not merely as a definition but as a requirement for mathematical coherence.
Zero Power in Real-World Applications
The rule a⁰ = 1 appears in physics, statistics, engineering, and computer science. Its presence often hides behind formulas, but it ensures the proper functioning of many systems.
In computer science, for example, algorithms frequently deal with exponent-based computations such as complexity analysis (O(n⁰) = O(1)). In physics, exponential decay formulas reduce to unity when time equals zero. In finance, compound interest formulas simplify to a⁰ = 1 when modeling the starting point of investment growth.
Here’s a table showing real-world formulas and where the 0-power appears:
| Field | Formula | Interpretation of Exponent 0 |
| Physics | N(t) = N₀e⁰ at t=0 | Ensures starting value equals N₀ |
| Finance | A = P(1 + r)⁰ | Ensures initial principal P is unchanged |
| Computer Science | O(n⁰) | Indicates constant-time operations |
| Statistics | x⁰ term in polynomials | Ensures the constant term is 1 |
Across fields, the rule provides stable initial conditions—a mathematical “reset point.”
The Subtlety of 0⁰: A Special Case
Though this article focuses on a⁰ for nonzero a, readers often wonder about the ambiguous expression 0⁰. In higher mathematics, its value depends on context. In combinatorics, 0⁰ is defined as 1 to maintain binomial expansion coherence. In analysis, 0⁰ is treated as an indeterminate form because limits of expressions like xˣ or (0.1)⁰ behave differently depending on the path of approach.
The essential distinction is this:
For any nonzero a, a⁰ = 1 always holds.
The special case 0⁰ involves competing definitions across domains.
The Unseen Beauty of Exponent Zero
A recurring theme in mathematics is that simplicity often masks depth. The rule a⁰ = 1 is deceptively short, almost throwaway in appearance, yet the underlying structure is immense. It sits at the intersection of multiple independent pathways: algebraic rules, combinatorics, calculus, and mathematical history. This convergence signals that the rule is not arbitrary but necessary.
When mathematicians extend concepts into new domains, they seek definitions that maintain consistency. The exponent zero acts as a stabilizing anchor—an invisible hinge on which countless formulas swing. Without it, fundamental calculations in engineering, physics, statistics, and computer science would become erratic.
Understanding 0 in this context transforms it from a passive placeholder into an active participant. The power of zero is, in many respects, the power that keeps mathematics itself coherent.
Takeaways
- The rule a⁰ = 1 is required to maintain consistent exponent laws.
- Patterns in decreasing exponents force the result logically.
- Combinatorics shows that an “empty choice” has exactly one outcome.
- Real-world formulas rely on a⁰ = 1 for correct initial values.
- Multiple mathematical fields independently converge on the same rule.
- Zero’s role in exponentiation is foundational, not arbitrary.
Conclusion
The quiet elegance of the exponent zero is easy to overlook, overshadowed by the complexity of higher powers and the visual drama of exponential growth. But a closer examination reveals that a⁰ = 1 is one of the most essential anchor points in the structure of mathematics. It ensures that patterns behave predictably, identities remain consistent, and the frameworks of analysis, algebra, and applied mathematics work together without contradiction. It is not merely a rule to memorize but a convergence point of logic, pattern, and mathematical necessity.
The significance of 0 becomes clearer when we appreciate how exponentiation extends across real numbers, negative powers, and fractional values. The zero exponent sits at a crossroads where definitions must work harmoniously or not at all. A world without a⁰ = 1 would be a fractured landscape, full of inconsistent results and broken formulas. Instead, mathematics maintains its coherence through this compact but powerful identity.
FAQs
Why does dividing by the base help explain a⁰ = 1?
Because decreasing an exponent by 1 always divides the expression by the base. Following this pattern down to zero forces the value to equal 1 for any nonzero base.
Does a⁰ = 1 apply to negative numbers?
Yes, as long as the base is nonzero. For instance, (–7)⁰ = 1.
Why is 0⁰ sometimes called indeterminate?
In calculus, the limit behaviors of functions approaching 0⁰ vary widely, making it an indeterminate form in analysis. But in combinatorics, 0⁰ = 1 is useful for counting.
Does the rule apply to irrational numbers?
Absolutely. π⁰, √2⁰, and e⁰ all equal 1 because the exponent rules apply universally to all nonzero real numbers.
Why do some students find the rule counterintuitive?
Because multiplying “nothing” by itself feels abstract. But the rule emerges from patterns and definitions that preserve consistency across mathematics.